| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 입문
- 백준
- 유니티
- 3월
- 코딩 테스트
- todolist
- 프로그래머스
- 4월
- 수학
- 단계별로 풀어보기
- 2022년
- 1월
- 게임 엔진 공부
- 5월
- 2024년
- 2023년
- 개인 프로젝트 - 런앤건
- 유니티 심화과정
- 10월
- 코딩 기초 트레이닝
- c++
- 6월
- 다이나믹 프로그래밍
- C/C++
- 골드메탈
- 자료 구조
- 2025년
- 기초
- 2월
- 개인 프로젝트
- Today
- Total
기록 보관소
[Baekjoon/백준] 2477번: 참외밭(C/C++) 본문
단계별로 풀어보기 14단계(누적 합) 4번 문제
https://www.acmicpc.net/step/50
기하 1 단계
도형이 배치된 모습을 잘 관찰하면서 아이디어를 얻는 문제
www.acmicpc.net
백준 2477번: 참외밭
https://www.acmicpc.net/problem/2477
2477번: 참외밭
첫 번째 줄에 1m2의 넓이에 자라는 참외의 개수를 나타내는 양의 정수 K (1 ≤ K ≤ 20)가 주어진다. 참외밭을 나타내는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지
www.acmicpc.net
문제 설명
시골에 있는 태양이의 삼촌 댁에는 커다란 참외밭이 있다. 문득 태양이는 이 밭에서 자라는 참외가 도대체 몇 개나 되는지 궁금해졌다. 어떻게 알아낼 수 있는지 골똘히 생각하다가 드디어 좋은 아이디어가 떠올랐다. 유레카! 1m2의 넓이에 자라는 참외 개수를 헤아린 다음, 참외밭의 넓이를 구하면 비례식을 이용하여 참외의 총개수를 구할 수 있다.
1m2의 넓이에 자라는 참외의 개수는 헤아렸고, 이제 참외밭의 넓이만 구하면 된다. 참외밭은 ㄱ-자 모양이거나 ㄱ-자를 90도, 180도, 270도 회전한 모양(┏, ┗, ┛ 모양)의 육각형이다. 다행히도 밭의 경계(육각형의 변)는 모두 동서 방향이거나 남북 방향이었다. 밭의 한 모퉁이에서 출발하여 밭의 둘레를 돌면서 밭경계 길이를 모두 측정하였다.

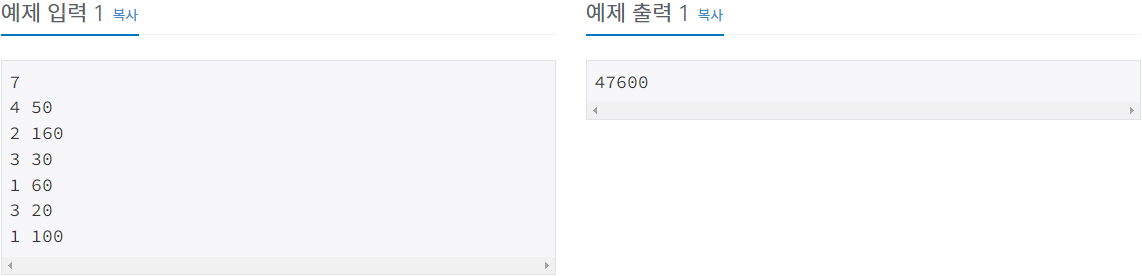
예를 들어 참외밭이 위 그림과 같은 모양이라고 하자. 그림에서 오른쪽은 동쪽, 왼쪽은 서쪽, 아래쪽은 남쪽, 위쪽은 북쪽이다. 이 그림의 왼쪽위 꼭짓점에서 출발하여, 반시계방향으로 남쪽으로 30m, 동쪽으로 60m, 남쪽으로 20m, 동쪽으로 100m, 북쪽으로 50m, 서쪽으로 160m 이동하면 다시 출발점으로 되돌아가게 된다.
위 그림의 참외밭 면적은 6800m2이다. 만약 1m2의 넓이에 자라는 참외의 개수가 7이라면, 이 밭에서 자라는 참외의 개수는 47600으로 계산된다.
1m2의 넓이에 자라는 참외의 개수와, 참외밭을 이루는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이가 순서대로 주어진다. 이 참외밭에서 자라는 참외의 수를 구하는 프로그램을 작성하시오.
입력과 출력
입력: 첫 번째 줄에 1m^2의 넓이에 자라는 참외의 개수를 나타내는 양의 정수 K (1 ≤ K ≤ 20)가 주어진다. 참외밭을 나타내는 육각형의 임의의 한 꼭짓점에서 출발하여 반시계방향으로 둘레를 돌면서 지나는 변의 방향과 길이 (1 이상 500 이하의 정수) 가 둘째 줄부터 일곱 번째 줄까지 한 줄에 하나씩 순서대로 주어진다. 변의 방향에서 동쪽은 1, 서쪽은 2, 남쪽은 3, 북쪽은 4로 나타낸다.
출력: 첫째 줄에 입력으로 주어진 밭에서 자라는 참외의 수를 출력한다.
접근 방법
이번 문제는 1m^2의 넓이에서 자라는 참외의 개수 K를 입력받고 육각형의 변의 방향(1 : 동쪽 | 2 : 서쪽 | 3 : 남쪽 | 4 : 북쪽)과 길이를 입력받아서 해당 밭에서 자라는 참외의 수를 출력하는 문제다.
문제 설명에서 임의의 한 꼭짓점을 출발해서 반시계 방향으로 변의 방향과 길이가 순서대로 주어진다고 했으므로, 변의 방향은 계속 번갈아가면서 주어지게 된다.
이를 이용하면 큰 직사각형에서 작은 직사각형을 빼는 방식으로 사각형의 너비를 구해 참외 개수를 구할 수 있을 것이다. 현재 길이와 다음 길이를 곱하는 방식으로 계속 크기를 구하고, 가장 넓은 값을 구하면 그 값에서 가장 작은 값을 빼고 그 값에 K(1m^2당 참외 개수)를 곱하면 그 값이 정답이 된다.
코드
#include <iostream>
using namespace std;
int direction[6];
int length[6];
int main(int argc, char * argv[]) {
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int K, max = 0, result = 0;
cin >> K;
for (int i = 0; i < 6; i++)
cin >> direction[i] >> length[i];
for (int i = 0; i < 6; i++) {
int num = length[i] * length[(i + 1) % 6];
if (num > max) {
max = num;
result = (max - length[(i + 3) % 6] * length[(i + 4) % 6]) * K;
}
}
cout << result << endl;
return 0;
}결과

'코딩 테스트 > 백준' 카테고리의 다른 글
| [Baekjoon/백준] 1358번: 하키(C/C++) (0) | 2022.07.13 |
|---|---|
| [Baekjoon/백준] 1004번: 어린 왕자(C/C++) (0) | 2022.07.12 |
| [Baekjoon/백준] 11660번: 구간 합 구하기 5(C/C++) (0) | 2022.07.06 |
| [Baekjoon/백준] 10986번: 나머지 합(C/C++) (0) | 2022.07.05 |
| [Baekjoon/백준] 16139번: 인간-컴퓨터 상호작용(C/C++) (0) | 2022.07.04 |




